Triangoło

In giometria, el triangoło el xe un połigono formà da tre angołi o vertisi e da tre lati; raprexenta ła figura co el minor numaro de lati, in quanto tre xe el numaro minimo de segmenti necesari par dełimitare na superficie sarà.

Carateristighe del triangoło

Il triangolo ze caratterizzato dalle seguenti proprietà:

Xe na figura indeformabiłe, a diferensa dei połigoni co un numaro magiore de lati; asegnae łe lunghese dei lati, o sia, łe xe univocamente determinài anca i angołi;
Xe l'unico połigono par cui nò'l xe domandà che sia regołare parché sia senpre posibiłe sircoscrivere e inscrivere na circonferensa, parché par tre punti pasa senpre una e una soła circonferensa;
Ła soma dei angołi interni xe uguałe a un angoło piato, ossia 180°; va comunque precixà che tałe uguajansa vałe soltanto inte ła giometria euclidea e nò in altri tipi de giometria come ła giometria sferica e queła iperbołica, 'ndove invese tałe soma xe, rispetivamente, magiore e minore de 180°;

Do triangołi i xe congruenti se i sodisfa almanco uno dei criteri de congruensa dei triangołi.

Do triangołi i se dixe simiłi se i sodifsa almanco uno dei criteri de similitudine.

Clasificasion dei triangołi

I triangołi i pol essare clasificài in baxe a ła longhesa rełativa dei lati:

In un triangoło equiłatero tuti i lati i gà longhesa uguałe. Un triangoło equiłatero se pol definire equivałentemente come triangoło equiangoło, overo triangoło che el gà i so angołi interni de uguałe anpiesa, pari a 60°.
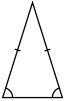
In un triangoło isoscele do lati i gà lpnghesa uguałe. Un triangoło isoscele se pol definire equivałentemente come triangolo che el gà do angołi interni de uguałe anpiesa.
In un triangoło scałeno tuti i lati i gà longhese difarenti. Un triangolo scałeno se pol definire equivałentemente come triangoło che el gà i tre angołi interni de diverse anpiese.


Equiłatero	Isoscele	Scałeno

I triangołi i pol essare clasificài anca in baxe a łe dimension del łoro angoło interno pì anpio; i xe descriti de seguito uxando i gradi d'arco.

Un triangoło retangoło (o triangoło reto) el gà un angoło interno de 90°, o sia un angoło reto. El lato oposto all'angoło reto xe ciamà ipotenuxa; xe el lato pì longo del triangoło retangoło. I altri do lati del triangoło i xe diti cateti. Par questo triangoło vałe el teorema de Pitagora.
Un [[triangoło otuxangoło (o triangoło otuxo) el gà un angoło interno magiore de 90°, o sia un angoło otuxo.
Un [[triangoło acutangoło (o triangoło acuto) el gà tuti i angołi interni minori de 90°, o sia gà tre angołi acuti.


Retangoło	Otuxangoło	Acutangoło

Formulario

Formułe trigonometriche

Se aplica ła trigonometria par catàr l'altesa h

L'area de un triangoło ła pol essare catà par via trigonometrica. Uxando łe letere de ła figura a destra, l'altesa h = a sen γ. Sostituendo questo inte ła formuła catà presedenteménte (par via giometrica), S = ½ab sen γ. L'area de un triangoło xe quindi anca uguałe al semiprodoto de do lati par el seno dell'angoło conprexo.

L'area del triangoło pol essare mixurà co ła formuła matemàtica:

$A={\frac {bh}{2}}$ 'ndove b xe ła baxe e h l'altesa a esa rełativa, parché el triangoło va visto come ła metà de un paralelograma de baxe b e altesa h.

opùr co $A={\sqrt {p*(p-a)*(p-b)*(p-c)}}$ 'ndove a, b e c i xe i lati e p el semiperimetro (Formuła de Erone).

Formułe anałitiche

Consideremo un triangoło ABC inte el piano cartexian individuà atraverso łe copie de coordinate dei vertisi $(x_{A},y_{A}),(x_{B},y_{B}),(x_{C},y_{C})$ .

Ła so area A e el so perimetro P i xe otenibiłi co łe espresioni

A={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{pmatrix}}\right|={\frac {1}{2}}{\big |}x_{A}(y_{B}-y_{C})-x_{B}(y_{A}-y_{C})+x_{C}(y_{A}-y_{B}){\big |}

opùre co na espresion che nò ła utiłixa el conceto de matrise

A=(x_{M}-x_{m})(y_{M}-y_{m})-({\frac {1}{2}}{\big |}x_{A}-x_{B}{\big |}{\big |}y_{A}-y_{B}{\big |}+{\frac {1}{2}}{\big |}x_{A}-x_{C}{\big |}{\big |}y_{A}-y_{C}{\big |}+{\frac {1}{2}}{\big |}x_{B}-x_{C}{\big |}{\big |}y_{B}-y_{C}{\big |})

'ndove

x_{M}=MAX{\big (}x_{A},x_{B},x_{C}{\big )}

x_{m}=MIN{\big (}x_{A},x_{B},x_{C}{\big )}

y_{M}=MAX{\big (}y_{A},y_{B},y_{C}{\big )}

y_{m}=MIN{\big (}y_{A},y_{B},y_{C}{\big )}

P={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}}}+{\sqrt {(x_{A}-x_{C})^{2}+(y_{A}-y_{C})^{2}}}+{\sqrt {(x_{B}-x_{C})^{2}+(y_{B}-y_{C})^{2}}}

Varda anca

Trigonometria
Sercio (altra figura giometrica)

Altri projeti

Wikimedia Commons el detien imàjini o altri file so triangoło
Scholia el detien schemi gràfeghi so Triangoło

Łigadure esterne

(EN) Triangle in MacTutor
(EN) Triangle Calculator - completes triangles when given three elements (sides, angles, area, height etc.), supports degrees, radians and grades.
(EN) Napoleon's theorem A triangle with three equilateral triangles. A purely geometric proof. It uses the Fermat point to prove Napoleon's theorem without transformations by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"

Controło de autorità	LCCN (EN) sh85137407 · BNF (FR) cb11946969k (data)