Integral

L'integral definìo de na funsion el corispónde a l'àrea sarà sù intrà el gràfico de ła funsion co ségno poxitivo quando che ła funsion el ga un vałor poxitivo e co ségno negativo quando che el ga vałor de negativo.

L' integral de na funsion, in anàłixi matemàtica, l'è un operator sviłupà orixinariamente par catar l'area sarà sù da ła curva de na funsion sul pian cartexian: el vien doparà parò in un saco de cunti, soratuto par problemi de fìxica. Drio el nùmaro de variàbiłi che ga ła funsion, l'integral el càlcoła l'area, el vołume, e.v.c...

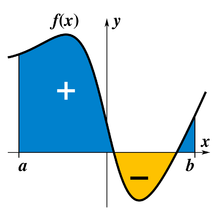
Ciapà na funsion f(x) co na variàbiłe reałe x e n'intervało [a,b] su ła reta reałe, l' integral

$\int _{a}^{b}f(x)\,dx$

l'è l'area del toco de pian cartexian sarà sù intrà el gràfico de f, l' ase x e łe lìnie verticałi x = a e x = b, manco l'area sóto l'ase x.

Ła paroła "integral" ła pol anca riferirse al conceto antiderivada oben primitiva, na funsion F che ła ga come derivada propio ła funsion f che se càlcoła l'integral. In 'sto caxo qua se ghe dixe integral indefinio, mentre che i integrałi che se parla qua i vien ciamai inegrałi definii: serti i fa difarensa intrà primitive e integrałi indefinii.

Altri progetti

• Wikimedia Commons

• Wikimedia Commons el detien imàjini o altri file so Integral
• el detien schemi gràfeghi so

Controło de autorità	LCCN (EN) sh85067099 · BNF (FR) cb119395946 (data)